GEOMETRIA ANALÍTICA
Convertendo a coordenada polar (2,  ) , em coordenada cartesianas, obtém-se a equação representada na alternativa:
) , em coordenada cartesianas, obtém-se a equação representada na alternativa:
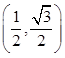
(3, 1)
( 1, 3)
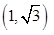
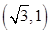
Identifique a equação da superfície hiperbolóide de uma folha de centro que possui as coordenadas (3, -1, -4) e cujo eixo encontra-se paralelo ao eixo Oy.
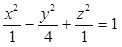
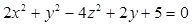
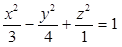
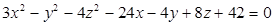
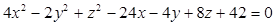
Assinale a alternativa que contém a equação da parábola de foco F(0,3) e reta diretriz de equação x – 2 = 0.
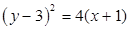
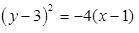
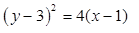
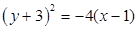
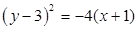
Pode-se afirmar que as coordenadas cartesianas do centro da hipérbole de equação 9x²-4y²-54x+8y+113=0 estão expressas em
(1, -3)
(1, 3)
(0, 3)
(3, 1)
(-3, -1)
Considere que A(-2, 1, 3) pertença ao plano  e que a reta
e que a reta 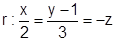 seja perpendicular a este plano . Neste caso, assinale a alternativa que contém a equação do plano
seja perpendicular a este plano . Neste caso, assinale a alternativa que contém a equação do plano  .
.
 :2x + 6y - z +4 = 0
:2x + 6y - z +4 = 0
 :2x + 3y - z -2 = 0
:2x + 3y - z -2 = 0
 :2x + 3y - z +6 = 0
:2x + 3y - z +6 = 0
 :2x + 3y - z +4 = 0
:2x + 3y - z +4 = 0
 : x + 3y - z +4 = 0
: x + 3y - z +4 = 0
Considere o ponto A(1,–2,1) e o vetor v =(3,1,4) que determinam a reta r. As equações vetoriais e paramétricas da reta r estão representadas, respectivamente, na alternativa
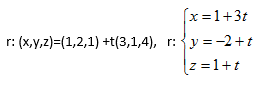
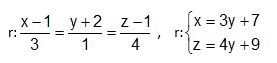
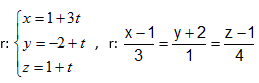

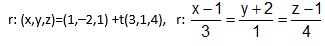
Dados os vetores u= ( 2,3,1) e v= ( 1,4, 5) . Assinale a alternativa que expressa o resultado do produto u.v.
24
-23
20
19
-19
Considerando os estudos sobre produtos entre vetores e dados os vetores u=( –1,3,2), v=(1,5,–2) e w=(-7,3,1) analise as afirmativas, a seguir:
I. u x v = (–16, 0, -8)
II. v x w = (11, 13, 38)
III. u . v = 20
IV. u.(v x w) = 104
V. (v x u) x w = (24, 0, 64)
É correto apenas o que se afirma em
I, II e III.
III, IV e V.
II, III e V.
I, II e IV.
I, IV e V.
Analise as afirmações feitas sobre a classificação dos pares de retas r : 6x+7y+3=0 e s: 12x+14y-21=0, e t: x+7y-10=0 e v : -7x+y-3=0 e assinale a alternativa correta.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.
Considere o triângulo ABC, onde A (2, 3), B (10, 9) e C (10, 3) representam as coordenadas dos seus vértices no plano de coordenadas cartesianas e M1 é o ponto médio do lado AB, M2 é o ponto médio do lado AC e M3 o ponto médio do lado BC. Com base nessas informações analise as afirmativas feitas, a seguir:
I. O ponto médio do lado AB tem coordenadas M1 =(6,6).
II. A medida do segmento M2B é igual a 6 u.m.
III. A medida do segmento M3A é igual a 5 u.m.
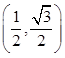
(3, 1)
( 1, 3)
![]()
![]()
Identifique a equação da superfície hiperbolóide de uma folha de centro que possui as coordenadas (3, -1, -4) e cujo eixo encontra-se paralelo ao eixo Oy.
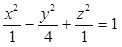
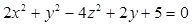
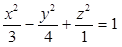
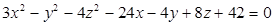
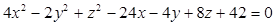
Assinale a alternativa que contém a equação da parábola de foco F(0,3) e reta diretriz de equação x – 2 = 0.
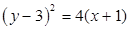
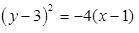
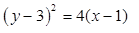
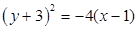
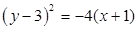
Pode-se afirmar que as coordenadas cartesianas do centro da hipérbole de equação 9x²-4y²-54x+8y+113=0 estão expressas em
(1, -3)
(1, 3)
(0, 3)
(3, 1)
(-3, -1)
Considere que A(-2, 1, 3) pertença ao plano  e que a reta
e que a reta 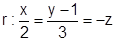 seja perpendicular a este plano . Neste caso, assinale a alternativa que contém a equação do plano
seja perpendicular a este plano . Neste caso, assinale a alternativa que contém a equação do plano  .
.
 :2x + 6y - z +4 = 0
:2x + 6y - z +4 = 0
 :2x + 3y - z -2 = 0
:2x + 3y - z -2 = 0
 :2x + 3y - z +6 = 0
:2x + 3y - z +6 = 0
 :2x + 3y - z +4 = 0
:2x + 3y - z +4 = 0
 : x + 3y - z +4 = 0
: x + 3y - z +4 = 0
Considere o ponto A(1,–2,1) e o vetor v =(3,1,4) que determinam a reta r. As equações vetoriais e paramétricas da reta r estão representadas, respectivamente, na alternativa
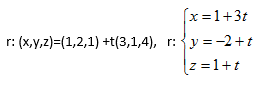
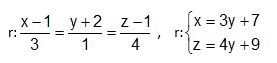
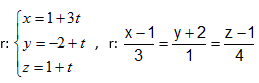

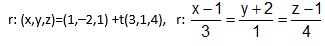
Dados os vetores u= ( 2,3,1) e v= ( 1,4, 5) . Assinale a alternativa que expressa o resultado do produto u.v.
24
-23
20
19
-19
Considerando os estudos sobre produtos entre vetores e dados os vetores u=( –1,3,2), v=(1,5,–2) e w=(-7,3,1) analise as afirmativas, a seguir:
I. u x v = (–16, 0, -8)
II. v x w = (11, 13, 38)
III. u . v = 20
IV. u.(v x w) = 104
V. (v x u) x w = (24, 0, 64)
É correto apenas o que se afirma em
I, II e III.
III, IV e V.
II, III e V.
I, II e IV.
I, IV e V.
Analise as afirmações feitas sobre a classificação dos pares de retas r : 6x+7y+3=0 e s: 12x+14y-21=0, e t: x+7y-10=0 e v : -7x+y-3=0 e assinale a alternativa correta.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.
Considere o triângulo ABC, onde A (2, 3), B (10, 9) e C (10, 3) representam as coordenadas dos seus vértices no plano de coordenadas cartesianas e M1 é o ponto médio do lado AB, M2 é o ponto médio do lado AC e M3 o ponto médio do lado BC. Com base nessas informações analise as afirmativas feitas, a seguir:
I. O ponto médio do lado AB tem coordenadas M1 =(6,6).
II. A medida do segmento M2B é igual a 6 u.m.
III. A medida do segmento M3A é igual a 5 u.m.
![]()
![]()
![]()
![]()
![]()
Assinale a alternativa que contém a equação da parábola de foco F(0,3) e reta diretriz de equação x – 2 = 0.
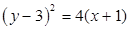
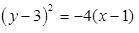
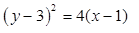
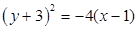
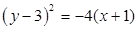
Pode-se afirmar que as coordenadas cartesianas do centro da hipérbole de equação 9x²-4y²-54x+8y+113=0 estão expressas em
(1, -3)
(1, 3)
(0, 3)
(3, 1)
(-3, -1)
Considere que A(-2, 1, 3) pertença ao plano  e que a reta
e que a reta 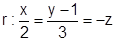 seja perpendicular a este plano . Neste caso, assinale a alternativa que contém a equação do plano
seja perpendicular a este plano . Neste caso, assinale a alternativa que contém a equação do plano  .
.
 :2x + 6y - z +4 = 0
:2x + 6y - z +4 = 0
 :2x + 3y - z -2 = 0
:2x + 3y - z -2 = 0
 :2x + 3y - z +6 = 0
:2x + 3y - z +6 = 0
 :2x + 3y - z +4 = 0
:2x + 3y - z +4 = 0
 : x + 3y - z +4 = 0
: x + 3y - z +4 = 0
Considere o ponto A(1,–2,1) e o vetor v =(3,1,4) que determinam a reta r. As equações vetoriais e paramétricas da reta r estão representadas, respectivamente, na alternativa
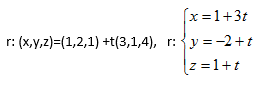
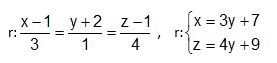
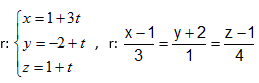

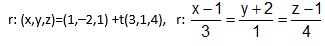
Dados os vetores u= ( 2,3,1) e v= ( 1,4, 5) . Assinale a alternativa que expressa o resultado do produto u.v.
24
-23
20
19
-19
Considerando os estudos sobre produtos entre vetores e dados os vetores u=( –1,3,2), v=(1,5,–2) e w=(-7,3,1) analise as afirmativas, a seguir:
I. u x v = (–16, 0, -8)
II. v x w = (11, 13, 38)
III. u . v = 20
IV. u.(v x w) = 104
V. (v x u) x w = (24, 0, 64)
É correto apenas o que se afirma em
I, II e III.
III, IV e V.
II, III e V.
I, II e IV.
I, IV e V.
Analise as afirmações feitas sobre a classificação dos pares de retas r : 6x+7y+3=0 e s: 12x+14y-21=0, e t: x+7y-10=0 e v : -7x+y-3=0 e assinale a alternativa correta.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.
Considere o triângulo ABC, onde A (2, 3), B (10, 9) e C (10, 3) representam as coordenadas dos seus vértices no plano de coordenadas cartesianas e M1 é o ponto médio do lado AB, M2 é o ponto médio do lado AC e M3 o ponto médio do lado BC. Com base nessas informações analise as afirmativas feitas, a seguir:
I. O ponto médio do lado AB tem coordenadas M1 =(6,6).
II. A medida do segmento M2B é igual a 6 u.m.
III. A medida do segmento M3A é igual a 5 u.m.
![]()
![]()
![]()
![]()
![]()
Pode-se afirmar que as coordenadas cartesianas do centro da hipérbole de equação 9x²-4y²-54x+8y+113=0 estão expressas em
(1, -3)
(1, 3)
(0, 3)
(3, 1)
(-3, -1)
Considere que A(-2, 1, 3) pertença ao plano  e que a reta
e que a reta 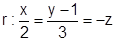 seja perpendicular a este plano . Neste caso, assinale a alternativa que contém a equação do plano
seja perpendicular a este plano . Neste caso, assinale a alternativa que contém a equação do plano  .
.
 :2x + 6y - z +4 = 0
:2x + 6y - z +4 = 0
 :2x + 3y - z -2 = 0
:2x + 3y - z -2 = 0
 :2x + 3y - z +6 = 0
:2x + 3y - z +6 = 0
 :2x + 3y - z +4 = 0
:2x + 3y - z +4 = 0
 : x + 3y - z +4 = 0
: x + 3y - z +4 = 0
Considere o ponto A(1,–2,1) e o vetor v =(3,1,4) que determinam a reta r. As equações vetoriais e paramétricas da reta r estão representadas, respectivamente, na alternativa
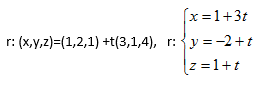
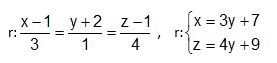
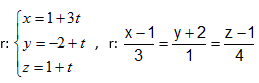

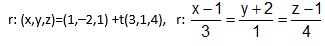
Dados os vetores u= ( 2,3,1) e v= ( 1,4, 5) . Assinale a alternativa que expressa o resultado do produto u.v.
24
-23
20
19
-19
Considerando os estudos sobre produtos entre vetores e dados os vetores u=( –1,3,2), v=(1,5,–2) e w=(-7,3,1) analise as afirmativas, a seguir:
I. u x v = (–16, 0, -8)
II. v x w = (11, 13, 38)
III. u . v = 20
IV. u.(v x w) = 104
V. (v x u) x w = (24, 0, 64)
É correto apenas o que se afirma em
I, II e III.
III, IV e V.
II, III e V.
I, II e IV.
I, IV e V.
Analise as afirmações feitas sobre a classificação dos pares de retas r : 6x+7y+3=0 e s: 12x+14y-21=0, e t: x+7y-10=0 e v : -7x+y-3=0 e assinale a alternativa correta.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.
Considere o triângulo ABC, onde A (2, 3), B (10, 9) e C (10, 3) representam as coordenadas dos seus vértices no plano de coordenadas cartesianas e M1 é o ponto médio do lado AB, M2 é o ponto médio do lado AC e M3 o ponto médio do lado BC. Com base nessas informações analise as afirmativas feitas, a seguir:
I. O ponto médio do lado AB tem coordenadas M1 =(6,6).
II. A medida do segmento M2B é igual a 6 u.m.
III. A medida do segmento M3A é igual a 5 u.m.
(1, -3)
(1, 3)
(0, 3)
(3, 1)
(-3, -1)
Considere que A(-2, 1, 3) pertença ao plano  e que a reta
e que a reta 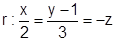 seja perpendicular a este plano . Neste caso, assinale a alternativa que contém a equação do plano
seja perpendicular a este plano . Neste caso, assinale a alternativa que contém a equação do plano  .
.
 :2x + 6y - z +4 = 0
:2x + 6y - z +4 = 0
 :2x + 3y - z -2 = 0
:2x + 3y - z -2 = 0
 :2x + 3y - z +6 = 0
:2x + 3y - z +6 = 0
 :2x + 3y - z +4 = 0
:2x + 3y - z +4 = 0
 : x + 3y - z +4 = 0
: x + 3y - z +4 = 0
Considere o ponto A(1,–2,1) e o vetor v =(3,1,4) que determinam a reta r. As equações vetoriais e paramétricas da reta r estão representadas, respectivamente, na alternativa
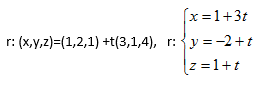
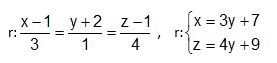
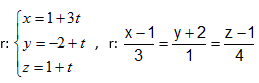

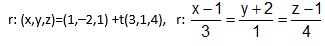
Dados os vetores u= ( 2,3,1) e v= ( 1,4, 5) . Assinale a alternativa que expressa o resultado do produto u.v.
24
-23
20
19
-19
Considerando os estudos sobre produtos entre vetores e dados os vetores u=( –1,3,2), v=(1,5,–2) e w=(-7,3,1) analise as afirmativas, a seguir:
I. u x v = (–16, 0, -8)
II. v x w = (11, 13, 38)
III. u . v = 20
IV. u.(v x w) = 104
V. (v x u) x w = (24, 0, 64)
É correto apenas o que se afirma em
I, II e III.
III, IV e V.
II, III e V.
I, II e IV.
I, IV e V.
Analise as afirmações feitas sobre a classificação dos pares de retas r : 6x+7y+3=0 e s: 12x+14y-21=0, e t: x+7y-10=0 e v : -7x+y-3=0 e assinale a alternativa correta.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.
Considere o triângulo ABC, onde A (2, 3), B (10, 9) e C (10, 3) representam as coordenadas dos seus vértices no plano de coordenadas cartesianas e M1 é o ponto médio do lado AB, M2 é o ponto médio do lado AC e M3 o ponto médio do lado BC. Com base nessas informações analise as afirmativas feitas, a seguir:
I. O ponto médio do lado AB tem coordenadas M1 =(6,6).
II. A medida do segmento M2B é igual a 6 u.m.
III. A medida do segmento M3A é igual a 5 u.m.
:2x + 6y - z +4 = 0
:2x + 3y - z -2 = 0
:2x + 3y - z +6 = 0
:2x + 3y - z +4 = 0
: x + 3y - z +4 = 0
Considere o ponto A(1,–2,1) e o vetor v =(3,1,4) que determinam a reta r. As equações vetoriais e paramétricas da reta r estão representadas, respectivamente, na alternativa
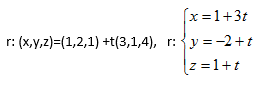
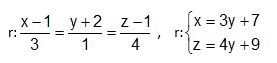
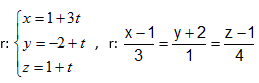

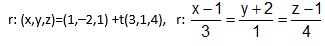
Dados os vetores u= ( 2,3,1) e v= ( 1,4, 5) . Assinale a alternativa que expressa o resultado do produto u.v.
24
-23
20
19
-19
Considerando os estudos sobre produtos entre vetores e dados os vetores u=( –1,3,2), v=(1,5,–2) e w=(-7,3,1) analise as afirmativas, a seguir:
I. u x v = (–16, 0, -8)
II. v x w = (11, 13, 38)
III. u . v = 20
IV. u.(v x w) = 104
V. (v x u) x w = (24, 0, 64)
É correto apenas o que se afirma em
I, II e III.
III, IV e V.
II, III e V.
I, II e IV.
I, IV e V.
Analise as afirmações feitas sobre a classificação dos pares de retas r : 6x+7y+3=0 e s: 12x+14y-21=0, e t: x+7y-10=0 e v : -7x+y-3=0 e assinale a alternativa correta.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.
Considere o triângulo ABC, onde A (2, 3), B (10, 9) e C (10, 3) representam as coordenadas dos seus vértices no plano de coordenadas cartesianas e M1 é o ponto médio do lado AB, M2 é o ponto médio do lado AC e M3 o ponto médio do lado BC. Com base nessas informações analise as afirmativas feitas, a seguir:
I. O ponto médio do lado AB tem coordenadas M1 =(6,6).
II. A medida do segmento M2B é igual a 6 u.m.
III. A medida do segmento M3A é igual a 5 u.m.
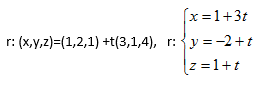
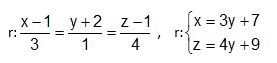
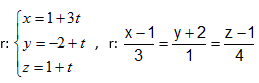

![]()
Dados os vetores u= ( 2,3,1) e v= ( 1,4, 5) . Assinale a alternativa que expressa o resultado do produto u.v.
24
-23
20
19
-19
Considerando os estudos sobre produtos entre vetores e dados os vetores u=( –1,3,2), v=(1,5,–2) e w=(-7,3,1) analise as afirmativas, a seguir:
I. u x v = (–16, 0, -8)
II. v x w = (11, 13, 38)
III. u . v = 20
IV. u.(v x w) = 104
V. (v x u) x w = (24, 0, 64)
É correto apenas o que se afirma em
I, II e III.
III, IV e V.
II, III e V.
I, II e IV.
I, IV e V.
Analise as afirmações feitas sobre a classificação dos pares de retas r : 6x+7y+3=0 e s: 12x+14y-21=0, e t: x+7y-10=0 e v : -7x+y-3=0 e assinale a alternativa correta.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.
Considere o triângulo ABC, onde A (2, 3), B (10, 9) e C (10, 3) representam as coordenadas dos seus vértices no plano de coordenadas cartesianas e M1 é o ponto médio do lado AB, M2 é o ponto médio do lado AC e M3 o ponto médio do lado BC. Com base nessas informações analise as afirmativas feitas, a seguir:
I. O ponto médio do lado AB tem coordenadas M1 =(6,6).
II. A medida do segmento M2B é igual a 6 u.m.
III. A medida do segmento M3A é igual a 5 u.m.
24
-23
20
19
-19
Considerando os estudos sobre produtos entre vetores e dados os vetores u=( –1,3,2), v=(1,5,–2) e w=(-7,3,1) analise as afirmativas, a seguir:
I. u x v = (–16, 0, -8)
II. v x w = (11, 13, 38)
III. u . v = 20
IV. u.(v x w) = 104
V. (v x u) x w = (24, 0, 64)
É correto apenas o que se afirma em
I, II e III.
III, IV e V.
II, III e V.
I, II e IV.
I, IV e V.
Analise as afirmações feitas sobre a classificação dos pares de retas r : 6x+7y+3=0 e s: 12x+14y-21=0, e t: x+7y-10=0 e v : -7x+y-3=0 e assinale a alternativa correta.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.
Considere o triângulo ABC, onde A (2, 3), B (10, 9) e C (10, 3) representam as coordenadas dos seus vértices no plano de coordenadas cartesianas e M1 é o ponto médio do lado AB, M2 é o ponto médio do lado AC e M3 o ponto médio do lado BC. Com base nessas informações analise as afirmativas feitas, a seguir:
I. O ponto médio do lado AB tem coordenadas M1 =(6,6).
II. A medida do segmento M2B é igual a 6 u.m.
III. A medida do segmento M3A é igual a 5 u.m.
I, II e III.
III, IV e V.
II, III e V.
I, II e IV.
I, IV e V.
Analise as afirmações feitas sobre a classificação dos pares de retas r : 6x+7y+3=0 e s: 12x+14y-21=0, e t: x+7y-10=0 e v : -7x+y-3=0 e assinale a alternativa correta.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.
Considere o triângulo ABC, onde A (2, 3), B (10, 9) e C (10, 3) representam as coordenadas dos seus vértices no plano de coordenadas cartesianas e M1 é o ponto médio do lado AB, M2 é o ponto médio do lado AC e M3 o ponto médio do lado BC. Com base nessas informações analise as afirmativas feitas, a seguir:
I. O ponto médio do lado AB tem coordenadas M1 =(6,6).
II. A medida do segmento M2B é igual a 6 u.m.
III. A medida do segmento M3A é igual a 5 u.m.
r e s não são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t não são perpendiculares.
r e s não são paralelas e v e t não são perpendiculares.
r e s são paralelas e v e t são perpendiculares.
r e s são paralelas e v e t são concorrentes e não perpendiculares.